Month: December 2016

Measuring V.2: Density and Arithmetic Progressions

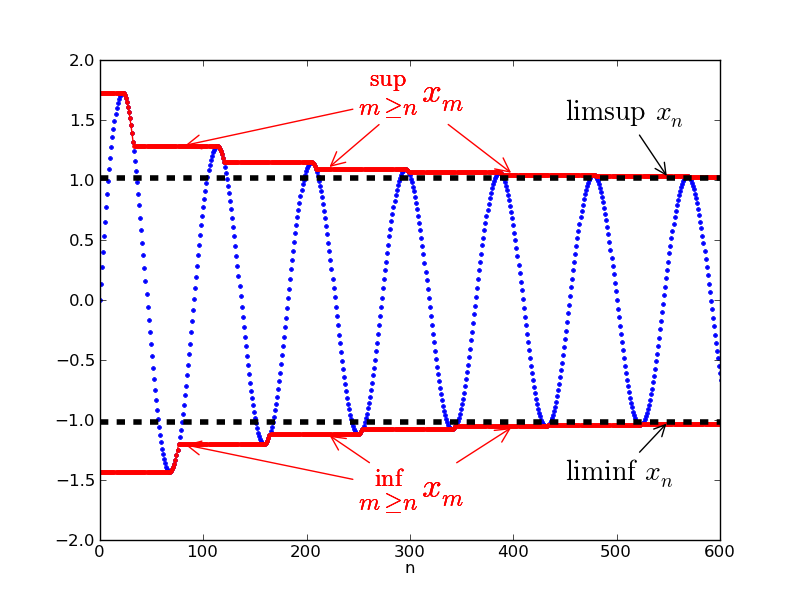
In our last post, we introduced the notions of density, upper density, and lower density as means of measuring subsets of natural numbers. We ended with two exercises. We recall them now; solutions are at the end of this post.

Exercise 1: Find subsets A,B \subseteq \mathbb{N} such that:

  • A \cap B = \emptyset;
  • A \cup B = \mathbb{N};
  • \overline{d}(A) = \overline{d}(B) = 1;
  • \underline{d}(A) = \underline{d}(B) = 0.

Exercise 2: Show that, if n \in \mathbb{N} and A_0, \ldots, A_n are subsets of \mathbb{N} such that A_0 \cup A_1 \cup \ldots \cup A_n = \mathbb{N}, then there is k \leq n such that \overline{d}(A_k) > 0.

Before getting to the solutions, though, let’s take an interesting detour through a simple topic that has been the focus of a large amount of groundbreaking mathematics over the last century: arithmetic progressions in natural numbers. The journey will stop at three beautiful theorems and one beautiful conjecture and will involve some of the mathematical giants of the twentieth and twenty-first centuries.

Definition: An arithmetic progression of natural numbers is an increasing sequence of natural numbers such that the difference between successive terms of the sequence is constant. The length of an arithmetic progression is the number of terms in the sequence.

For example, the sequence \langle 4,7,10,13 \rangle is an arithmetic progression of length 4, as the difference between each pair of successive terms is 3. The sequence of even numbers, \langle 0,2,4,6,\ldots \rangle, and the sequence of odd numbers, \langle 1,3,5,7, \ldots \rangle are both arithmetic progressions of infinite length.

In an earlier post, we introduced the mathematical field of Ramsey Theory. Roughly speaking, Ramsey Theory studies the phenomenon of order necessarily arising in sufficiently large structures. Ramsey Theory takes its name from Frank Ramsey, who published a seminal paper in 1930. Arguably the first important theorem in Ramsey Theory, though, came three years earlier and is due to the Dutch mathematician Bartel Leendert van der Waerden.

noethervanderwaerden1979
Bartel van der Waerden

Theorem (van der Waerden, 1927): Suppose that the natural numbers are partitioned into finitely many sets, A_0, A_1, \ldots, A_n (so we have \bigcup_{i \leq n} A_i = \mathbb{N}). Then there is an i \leq n such that A_i contains arithmetic progressions of every finite length.

This is naturally seen as a statement in Ramsey Theory: Arithmetic progressions are very orderly things, and Van der Waerden’s Theorem states that, no matter how deviously you divide the natural numbers into finitely many pieces, you cannot avoid the appearance of arbitrarily long arithmetic progressions in one of the pieces. It is also worth noting that Van der Waerden’s Theorem cannot be strengthened to ensure the existence of infinite arithmetic progressions: it is relatively easy to partition the natural numbers into even just two sets such that neither set contains an arithmetic progression of infinite length (try it!).

You might notice a similarity between the statement of Van der Waerden’s Theorem and our Exercise 2: both say that, if the natural numbers are divided into finitely many pieces, at least one of the pieces must be “large” in a certain sense. In Van der Waerden’s Theorem, “large” means containing arbitrarily long arithmetic progressions, while in Exercise 2, it means having positive upper density.

Is there a connection between these two notions of largeness? It turns out that there is! In 1936, Erdős and Turán conjectured that, if A \subseteq \mathbb{N} and A has positive density, then A contains arbitrarily long arithmetic progressions. Almost forty years later, the conjecture was confirmed (and, in fact, strengthened, as it was proven for upper density rather than density) in a celebrated proof by Hungarian mathematician Endre Szemerédi.

szemeredi
Endre Szemerédi

Theorem (Szemerédi, 1975): Suppose that A \subseteq \mathbb{N} and \overline{d}(A) > 0. Then A contains arithmetic progressions of every finite length.

Note that Szemerédi’s Theorem is a true generalization and strengthening of Van der Waerden’s theorem: when combined with Exercise 2, Szemerédi’s Theorem directly implies Van der Waerden’s Theorem. However, Szemerédi’s Theorem does not give any information about sets of natural numbers with zero upper density. There is one particularly interesting such set, which we encountered in our last post: the set of prime numbers, P = \{2,3,5,7,11, \ldots \}.

According to experts, it is likely that it was conjectured as early as 1770, by Lagrange and Waring, that the set of primes contains arbitrarily long arithmetic progressions, and the question experienced renewed interest in the wake of the proof of Szemerédi’s Theorem. An answer finally came in 2004, in a paper by Ben Green and Terence Tao.

Theorem (Green-Tao, 2004): The set of prime numbers contains arithmetic progressions of every finite length.

The story has not ended yet, as many very natural questions about arithmetic progressions remain unsolved. Perhaps the most famous is the following conjecture of Erdős, strengthening his conjecture with Turán that was eventually confirmed by Szemerédi.

Conjecture (Erdős): Suppose A \subseteq \mathbb{N} (with 0 \not\in A) and \sum_{n \in A} \frac{1}{n} = \infty. Then A arithmetic progressions of every finite length.

This conjecture, unlike Szemerédi’s Theorem, would cover the case in which A is the set of all primes, so this conjecture would generalize both Szemerédi’s Theorem and the Green-Tao Theorem. The problem currently carries a cash prize of $5000 (and, of course, the promise of mathematical fame).

Solution to Exercise 1: Recursively define a sequence \langle a_n \mid n \in \mathbb{N} \rangle by letting a_0 = 1, and, given a_0, \ldots, a_n, letting a_{n+1} = (n+1)(a_0 + a_1 + \ldots + a_n). The first few terms of the sequence are thus 1,1,4,18,96, \ldots. Now divide \mathbb{N} into pairwise disjoint blocks \langle A_n \mid n \in \mathbb{N} \rangle, arranged one after the other, in which, for all n \in \mathbb{N}, |A_n| = a_n. The first few blocks are thus as follows:

  • A_0 = \{0\};
  • A_1 = \{1\};
  • A_2 = \{2,3,4,5\};
  • A_3 = \{6,7,\ldots,23\};
  • A_4 = \{24,25,\ldots,119\}.

Now let A be the union of all of the even-numbered blocks, i.e. A = \bigcup_{n \in \mathbb{N}}A_{2n}, and let B be the union of all of the odd-numbered blocks.

We clearly have A \cap B = \emptyset and A \cup B = \mathbb{N}. We next show \overline{d}(A) = 1. Recall that \overline{d}(A) = \limsup_{n \rightarrow \infty} \frac{|A \cap n|}{n}. Given n \in \mathbb{N}, let m_n be the largest element of A_{2n}. Think about the quantity \frac{|A \cap (m_n+1)|}{m_n+1}. Since A_{2n} \subseteq A, we clearly have |A \cap (m_n+1)| \geq |A_{2n}| = a_{2n}. We also have m_n+1 = |A_0| + |A_1| + \ldots + |A_{2n}| = a_0 + a_1 + \ldots + a_{2n}. But this yields:

\frac{|A \cap (m_n+1)|}{m_n+1} \geq \frac{a_{2n}}{a_0 + \ldots + a_{2n}} = \frac{(2n)(a_0 + \ldots + a_{2n-1})}{a_0 + \ldots + a_{2n-1} + (2n)(a_0 + \ldots + a_{2n-1})} = \frac{2n}{2n+1}.

As n gets arbitrarily large, \frac{2n}{2n+1} gets arbitrarily close to 1, so we in fact get \overline{d}(A) = 1. The proofs of \overline{d}(B) = 1 and \underline{d}(A) = \underline{d}(B) = 0 are essentially the same and are thus left to the reader.

Solution to Exercise 2: We will in fact show something stronger: there is k \leq n such that \overline{d}(A_k) \geq \frac{1}{n+1}. Suppose for sake of a contradiction that this is not the case. Then, by the definition of upper density, for each k \leq n we can find m_k \in \mathbb{N} such that, for all natural numbers m \geq m_k, \frac{|A_k \cap m|}{m} < \frac{1}{n+1}. Now we can choose a natural number m^* large enough so that, for all k \leq n, m_k \leq m^*.

For each k \leq n, by our choice of m_k, we know that \frac{|A_k \cap m^*|}{m^*} < \frac{1}{n+1}. Also, by the fact that A_0 \cup \ldots \cup A_n = \mathbb{N}, we have that |A_0 \cap m^*| + \ldots + |A_n \cap m^*| \geq m^*. But this yields:

1 = \frac{m^*}{m^*} \leq \frac{|A_0 \cap m^*| + \ldots + |A_n \cap m^*|}{m^*} = \frac{|A_0 \cap m^*|}{m^*} + \ldots + \frac{|A_n \cap m^*|}{m^*} <

<\frac{1}{n+1} + \ldots + \frac{1}{n+1} = (n+1)\frac{1}{n+1} = 1.

We have thus shown 1 < 1. This is, of course, a contradiction, which finishes the exercise.

Cover Image: Vir Heroicus Sublimis by Barnett Newman

Posted on by Chris Lambie-Hanson 0

Measuring V.1: Density

In a previous installment of our Measuring series, we considered the question of measuring subsets of the natural numbers. We came up with a solution using a non-principal ultrafilter. This is an elegant solution, but it has some drawbacks. One of these is that, assuming we are assigning a measure of 1 to the entire set, it seems natural to want to assign a measure of \frac{1}{2} to both the set of even numbers and the set of odd numbers. However, depending on which of these two sets is in our ultrafilter, the ultrafilter measure will assign a measure of 1 to one of these sets and 0 to the other. We discussed an ad hoc fix to this, but, even then, similar problems arise. The ultrafilter measure is simply not what we want in many instances.

Today, we are going to discuss another approach to thinking about the size of subsets of \mathbb{N}, an approach that exploits the fact that it is really easy to measure subsets of a finite set. Our strategy will be to approximate the natural numbers by larger and larger finite sets, which we can easily deal with, and then see if their behavior converges to a limit.

Recall that, given a natural number n, we think of n as the set of all smaller natural numbers, i.e. n = \{0,1,\ldots,n-1\}. Given a subset A \subseteq \mathbb{N} and a natural number n, let

d_n(A) = \frac{|A \cap n|}{n}.

d_n(A) thus gives us the measure of A relative to the first n natural numbers. We might hope that, as n gets larger, we get better and better information about the distribution of A. This happens precisely when the limit \lim_{n \rightarrow \infty} d_n(A) exists. When it does, we let d(A) = \lim_{n \rightarrow \infty} d_n(A). (For those of you who forget pre-calculus, recall that, intuitively, \lim_{n \rightarrow \infty} d_n(A) = L if, as n gets larger and larger, d_n(A) gets closer and closer to L.)

d(A), when it exists, is called the asymptotic density of A. Asymptotic density can be a useful way of measuring subsets of \mathbb{N}, and it has some nice properties. For example, the following are easily seen.

  • d(\emptyset) = 0.
  • d(\mathbb{N}) = 1.
  • d(\mathrm{Evens}) = d(\mathrm{Odds}) = \frac{1}{2}.

The celebrated Prime Number Theorem states that, asymptotically, d_n(\mathrm{Primes}) \sim \frac{1}{\log(n)}. Therefore, since \log(n) gets arbitrarily large as n increases, we immediately get d(\mathrm{Primes}) = 0.

Asymptotic density also has the nice feature of being finitely additive. This means that, if A,B \subseteq \mathbb{N}, A \cap B = \emptyset, and d(A) and d(B) both exist, then d(A \cup B) exists and d(A \cup B) = d(A) + d(B).

A big drawback to asymptotic density, though, is that, in general, there is no guarantee that the limit \lim_{n \rightarrow \infty} d_n(A) will exist. Thus, for many sets A \subseteq \mathbb{N}, d(A) is simply undefined. This leads us to consider generalizations of asymptotic density, called upper and lower density, that will be defined for more sets (in fact, for all of them). To do so, we need to review some key facts about real numbers.

Recall that [0,1] denotes the closed interval of real numbers r such that 0 \leq r \leq 1. If X \subseteq [0,1], then the supremum of X, denoted \sup(X), is the least real number s such that, for all r \in X, r \leq s. Intuitively, \sup(X) is the least real number that bounds X from above. Dually, the infimum of X, denoted \inf(X), is the largest real number s such that, for all r \in X, s \leq r. \inf(X) is thus the largest real number that bounds X from below. It is one of the defining features of the real numbers that suprema and infima of bounded sets always exist.

Now suppose we have a sequence \langle x_n \mid n \in \mathbb{N} \rangle, where, for all n, x_n \in \mathbb{R}. The limit \lim_{n \rightarrow \infty}x_n might fail to exist; for example, this will be the case if the sequence oscillates between two different numbers. To help analyze the behavior of bounded sequences without limits, we can consider variations on the limit, known as the limit superior (\limsup) and limit inferior (\liminf). These are defined as follows:

\limsup_{n \rightarrow \infty} = \lim_{n \rightarrow \infty}(\sup\{x_m \mid m \geq n\})

\liminf_{n \rightarrow \infty} = \lim_{n \rightarrow \infty}(\inf\{x_m \mid m \geq n\})

Take a minute to think about what these definitions are saying. The following image may be useful.

Lim sup example 5.png
By Eigenjohnson – Own work, CC BY-SA 3.0, Link

It should be noted that \limsup_{n \rightarrow \infty} x_n is the limit of a non-increasing sequence and \liminf_{n \rightarrow \infty} x_n is the limit of a non-decreasing sequence, so both of them are guaranteed to exist (if the sequence is not bounded, one or both might be \pm \infty).

With this in mind, we can now define the upper density of a set A \subseteq \mathbb{N} to be:

\overline{d}(A) = \limsup_{n \rightarrow \infty} d_n(A)

and the lower density to be:

\underline{d}(A) = \liminf_{n \rightarrow \infty} d_n(A).

Upper and lower density have the nice feature that they are defined for all subsets of natural numbers. In addition, it is easily seen that, if A \subseteq \mathbb{N} and d(A) exists, then \overline{d}(A) = d(A) = \underline{d}(A). Upper and lower density can be useful ways of quantifying the “size” of subsets of \mathbb{N}. In particular, as we will see in our next post, the statement \overline{d}(A) > 0 can in many contexts be interpreted as stating that A is a “non-negligible” subset of \mathbb{N}.

However, upper and lower density suffer from a fatal flaw that prevents them from being considered to be true “measures” of subsets of \mathbb{N}: they are not even finitely additive. I leave you for now to explore this phenomenon on your own; solutions to the following two exercises and further investigation of density will come next week.

Exercise 1: Find subsets A,B \subseteq \mathbb{N} such that:

  • A \cap B = \emptyset;
  • A \cup B = \mathbb{N};
  • \overline{d}(A) = \overline{d}(B) = 1;
  • \underline{d}(A) = \underline{d}(B) = 0.

Exercise 2: Show that, if n \in \mathbb{N} and A_1, A_2, \ldots, A_n are subsets of \mathbb{N} such that A_1 \cup A_2 \cup \ldots \cup A_n = \mathbb{N}, then there is k \leq n such that \overline{d}(A_k) > 0.

Cover image: Wallace Bournes by Gerhard Richter

Posted on by Chris Lambie-Hanson 1