In our previous post, we took a detour to consider the shape of space. Today, we return to time, both external and personal, and the question, “What does it mean to be immortal?”
The distinction between external time and personal time was introduced by Lewis in his 1976 paper, “The Paradoxes of Time Travel.” The term “external time” refers to time itself. “Personal time,” applied to a particular person, is, as Lewis puts it, “roughly, that which is measured by his wristwatch.” It might be more precise to think of personal time as the time measured by one’s internal processes: if, in a period of external time, I go through the physical processes that a typical person would go through in an hour, then, during that period of external time, one hour of personal time has elapsed for me.
In the common view of time, it is shaped like a straight line, stretching infinitely far in front of us. (We will be agnostic here about whether or not infinitely much time has already elapsed.) In this view, the years lying ahead of us form an  -sequence, i.e., a sequence ordered like the natural numbers. This year could be called Year 0, next year Year 1, and so on. One natural number for each future year, and one future year for each natural number. Also, in human experience thus far, external time and personal time have pretty much lined up. With this simple view of time and of the relationship between external and personal time, it is also pretty simple to see what it means to be immortal: a person is immortal if they live for all of the years after they are born.
-sequence, i.e., a sequence ordered like the natural numbers. This year could be called Year 0, next year Year 1, and so on. One natural number for each future year, and one future year for each natural number. Also, in human experience thus far, external time and personal time have pretty much lined up. With this simple view of time and of the relationship between external and personal time, it is also pretty simple to see what it means to be immortal: a person is immortal if they live for all of the years after they are born.
This simple view of immortality probably suffices for practical discussions about its feasibility and desirability. Right now, though, we’re going to indulge ourselves in a bit of conceptual analysis, contemplating improbable thought experiments with the aim of gaining a fuller understanding of immortality or, at the very least, having some fun trying. Today: transfinite life.

In a delightful 1985 paper, entitled “On Living Forever,” Phillip Bricker argues that he wants not just to live for an infinite number of years, but to live for a transfinite number of years, i.e., more than one  -sequence of years. Even if our universe happens to only have an
-sequence of years. Even if our universe happens to only have an  -sequence of years in the future, Bricker argues, it is conceivable that there are universes with more than an
-sequence of years in the future, Bricker argues, it is conceivable that there are universes with more than an  -sequence of years, and it would be desirable to live in such a universe and live for a transfinite number of years.
-sequence of years, and it would be desirable to live in such a universe and live for a transfinite number of years.
There are a number of points to be considered here. For simplicity, let’s say there is a universe with two  -sequences of years, one after the other, and that we are currently considering the beginning of the first of these two
-sequences of years, one after the other, and that we are currently considering the beginning of the first of these two  -sequences. Let us call this year Year 0A, next year Year 1A, the following year Year 2A, and so on, defining Year NA for every natural number N. After this
-sequences. Let us call this year Year 0A, next year Year 1A, the following year Year 2A, and so on, defining Year NA for every natural number N. After this  -sequence of years, there will be the start of the second
-sequence of years, there will be the start of the second  -sequence. Let us call the first year of this sequence Year 0B, the next year Year 1B, and so on.
-sequence. Let us call the first year of this sequence Year 0B, the next year Year 1B, and so on.
The first and most fundamental question is perhaps, “Is this possible? Does this make sense?” More precisely, can the universe of the second  -sequence of years really be considered the “same” universe as that of the first
-sequence of years really be considered the “same” universe as that of the first  -sequence of years? Can a universe extend across multiple
-sequence of years? Can a universe extend across multiple  -sequences of years? Bricker answers this question affirmatively with a process that might be called “decompression.” He asks the reader to consider the events between 11 PM and midnight on December 31, 1999. There is a possible world, he says, in which the events between 11 and 11:30 take one year to occur, the events between 11:30 and 11:45 take one year to occur, and so on, so that the events of this hour in our world take an entire
-sequences of years? Bricker answers this question affirmatively with a process that might be called “decompression.” He asks the reader to consider the events between 11 PM and midnight on December 31, 1999. There is a possible world, he says, in which the events between 11 and 11:30 take one year to occur, the events between 11:30 and 11:45 take one year to occur, and so on, so that the events of this hour in our world take an entire  -sequence of years in this other world. After midnight, the two worlds proceed at the same rate. Thus, if our world has one
-sequence of years in this other world. After midnight, the two worlds proceed at the same rate. Thus, if our world has one  -sequence of years, this other world has two. Moreover, whatever relations hold between our world pre-midnight and our world post-midnight hold between the first
-sequence of years, this other world has two. Moreover, whatever relations hold between our world pre-midnight and our world post-midnight hold between the first  -sequence of the other world and the second
-sequence of the other world and the second  -sequence of the other world. So, Bricker argues, the extension of a possible universe across multiple
-sequence of the other world. So, Bricker argues, the extension of a possible universe across multiple  -sequences of years is no more mysterious than the extension of our universe across multiple days.
-sequences of years is no more mysterious than the extension of our universe across multiple days.
I admit that this is a somewhat convincing argument, but I find it only convincing of the possibility of a transfinite universe of a very particular sort, namely of a sort that respects some continuity conditions. In the world in which the events of an hour in our world take an entire  -sequence of years, things that proceed at a steady pace in our world proceed increasingly slowly. The world undergoes less and less change as this
-sequence of years, things that proceed at a steady pace in our world proceed increasingly slowly. The world undergoes less and less change as this  -sequence progresses. In a very precise sense, as these infinitely many years go on, this alternate world converges to a fixed limit. This limit, of course, is the state of our world at midnight, which is the state of the alternate world at the start of the second
-sequence progresses. In a very precise sense, as these infinitely many years go on, this alternate world converges to a fixed limit. This limit, of course, is the state of our world at midnight, which is the state of the alternate world at the start of the second  -sequence. Such a world, though, is a rather uninteresting example of a transfinite universe and would not be particularly appealing for somebody looking for true transfinite immortality. For suppose that such a person lived in this world for both
-sequence. Such a world, though, is a rather uninteresting example of a transfinite universe and would not be particularly appealing for somebody looking for true transfinite immortality. For suppose that such a person lived in this world for both  -sequences of years. As the first
-sequences of years. As the first  -sequence went on, everything would slow down, including the person’s movements, internal processes, thoughts. At the end of the first
-sequence went on, everything would slow down, including the person’s movements, internal processes, thoughts. At the end of the first  -sequence, even if infinitely many years of external time had occurred, the person’s experiences would only be equivalent to a finite amount of personal time in our world. So this person, living for two
-sequence, even if infinitely many years of external time had occurred, the person’s experiences would only be equivalent to a finite amount of personal time in our world. So this person, living for two  -sequences of years, would have the same experience as someone living for one
-sequences of years, would have the same experience as someone living for one  -sequene of years in our world, defeating the purpose of wanting a transfinite existence in the first place.
-sequene of years in our world, defeating the purpose of wanting a transfinite existence in the first place.
To illustrate the difficulty, let’s consider a universe, called Universe T, with two  -sequences of years, that definitely does not converge, using a classic thought experiment known as Thomson’s Lamp, which we briefly visited in an earlier post in connection with Zeno’s paradoxes. Let’s suppose that you are living in this world, in the first
-sequences of years, that definitely does not converge, using a classic thought experiment known as Thomson’s Lamp, which we briefly visited in an earlier post in connection with Zeno’s paradoxes. Let’s suppose that you are living in this world, in the first  -sequence. Let’s suppose moreover that you live for the entire first
-sequence. Let’s suppose moreover that you live for the entire first  -sequence, spending all of the years living in the same house. On your bedside table is a lamp that, miraculously, never breaks and never needs a replacement bulb. Every morning, when you wake, you turn the lamp on, and every night, when you go to bed, you turn the lamp off. Now: at the first moment of the second
-sequence, spending all of the years living in the same house. On your bedside table is a lamp that, miraculously, never breaks and never needs a replacement bulb. Every morning, when you wake, you turn the lamp on, and every night, when you go to bed, you turn the lamp off. Now: at the first moment of the second  -sequence of years, is the lamp on or off? (Does the lamp even exist?) It seems impossible to answer this question, or even to make sense of it. If it were the case that, from a certain point onward in the first
-sequence of years, is the lamp on or off? (Does the lamp even exist?) It seems impossible to answer this question, or even to make sense of it. If it were the case that, from a certain point onward in the first  -sequence of years, the lamp were off, then it would be natural to answer that the lamp is off at the start of second
-sequence of years, the lamp were off, then it would be natural to answer that the lamp is off at the start of second  -sequence, and similarly if the lamp were on from a certain point. In this case, though, the lamp does not converge to any single state, so it is hard to see what will happen to it in the second
-sequence, and similarly if the lamp were on from a certain point. In this case, though, the lamp does not converge to any single state, so it is hard to see what will happen to it in the second  -sequence.
-sequence.
In order to use Bricker’s argument to argue for the plausibility of this world, we would want to apply the opposite of “decompression,” something a person might reasonably call “compression.” To do this, we would want to consider a world, called Universe S, in which the first year’s events in Universe T take half an hour, the second year’s events in Universe T take a quarter of an hour, and so on, so that the events of the first  -sequence of years in Universe T take one hour in Universe S. Now, one wants to say, there is no problem with Universe S lasting for more than one hour, so, to figure out what happened to your lamp at the start of the second
-sequence of years in Universe T take one hour in Universe S. Now, one wants to say, there is no problem with Universe S lasting for more than one hour, so, to figure out what happened to your lamp at the start of the second  -sequence in Universe T, just look at its state at the start of the second hour in Universe S. There is an issue here, though. In compressing the events of the first
-sequence in Universe T, just look at its state at the start of the second hour in Universe S. There is an issue here, though. In compressing the events of the first  -sequence of Universe T into one hour, certain things, such as the turning on and off of the lamp, happen at faster and faster speeds, indeed at speeds approaching infinity. This would of course be a problem in our universe, in which nothing can travel faster than the speed of light. It might be a problem in every universe. Are there possible universes in which objects can travel arbitrarily fast? If so, what would these universes be like? Are these thought experiments entirely misguided in the first place and driven by inaccurate conceptions of time? These questions certainly lie beyond the scope of this post. For now, let’s just leave them here as possible difficulties in justifying the possibility of interesting transfinite universes.
-sequence of Universe T into one hour, certain things, such as the turning on and off of the lamp, happen at faster and faster speeds, indeed at speeds approaching infinity. This would of course be a problem in our universe, in which nothing can travel faster than the speed of light. It might be a problem in every universe. Are there possible universes in which objects can travel arbitrarily fast? If so, what would these universes be like? Are these thought experiments entirely misguided in the first place and driven by inaccurate conceptions of time? These questions certainly lie beyond the scope of this post. For now, let’s just leave them here as possible difficulties in justifying the possibility of interesting transfinite universes.

Let’s put aside any objections, though, and suppose that there can in fact be a world spanning multiple  -sequences of years and that a person could exist across these multiple
-sequences of years and that a person could exist across these multiple  -sequences in such a way that their personal time would coincide with the external time. Would this in fact be better than simply living for one
-sequences in such a way that their personal time would coincide with the external time. Would this in fact be better than simply living for one  -sequence? Bricker’s primary reason for answering affirmatively is simply that he wants the pleasures of life (for example, eating Thai food) to be experienced as many times as possible. Eating Thai food provides pleasure; why limit oneself to just an
-sequence? Bricker’s primary reason for answering affirmatively is simply that he wants the pleasures of life (for example, eating Thai food) to be experienced as many times as possible. Eating Thai food provides pleasure; why limit oneself to just an  -sequence of Thai meals? Why not two
-sequence of Thai meals? Why not two  -sequences of Thai meals? Why not uncountably many Thai meals? Inaccessibly many Thai meals? A supercompact number of Thai meals? The more the better!
-sequences of Thai meals? Why not uncountably many Thai meals? Inaccessibly many Thai meals? A supercompact number of Thai meals? The more the better!
Another intriguing reason offered by Bricker involves the pursuit of mathematical knowledge. There are unsolved problems in number theory, for example, which could easily be solved in an infinite amount of time simply by checking every number. For example, the Goldbach conjecture, unproven to this day, asserts that every even number greater than 2 can be expressed as the sum of two prime numbers. The conjecture has resisted many attempts at proof by some of the great mathematicians of the world, but, if someone were able to live for more than an  -sequence of years, they could prove or refute it very easily: during the first
-sequence of years, they could prove or refute it very easily: during the first  -sequence of years, they could systematically check every even number. If they find one that cannot be expressed as the sum of two prime numbers, they write it down as a counterexample, disproving the conjecture. If, after the first
-sequence of years, they could systematically check every even number. If they find one that cannot be expressed as the sum of two prime numbers, they write it down as a counterexample, disproving the conjecture. If, after the first  -sequence of years, they have not written down a counterexample, they will know that there is none, and the conjecture is true.
-sequence of years, they have not written down a counterexample, they will know that there is none, and the conjecture is true.
Let’s note a couple of potential issues here. First, humans have finite brains. So, suppose that someone lives for longer than one  -sequence of years. When they wake up in Year 0B, the first year of the second
-sequence of years. When they wake up in Year 0B, the first year of the second  -sequence, they will only be able to remember finitely many things from the first
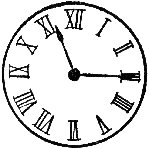
-sequence, they will only be able to remember finitely many things from the first  -sequence. Thus, as far as their memory is concerned, they will essentially only have lived for a finite number of years. This brings up two questions. First, will they be able to tell that it is Year 0B? If they cannot remember anything past Year 100A, then, as far as they are concerned, it might as well be Year 101A. There are obvious external remedies for this. For example, perhaps they could fashion a clock that moves from 12 to 6 during one year, 6 to 9 during the next, 9 to 10:30 during the next, and so on, so that the clock returning to 12 will mark the end of the first
-sequence. Thus, as far as their memory is concerned, they will essentially only have lived for a finite number of years. This brings up two questions. First, will they be able to tell that it is Year 0B? If they cannot remember anything past Year 100A, then, as far as they are concerned, it might as well be Year 101A. There are obvious external remedies for this. For example, perhaps they could fashion a clock that moves from 12 to 6 during one year, 6 to 9 during the next, 9 to 10:30 during the next, and so on, so that the clock returning to 12 will mark the end of the first  -sequence of years.
-sequence of years.
Secondly, and perhaps more seriously, suppose that this person engaged themselves in solving Goldbach’s Conjecture by checking all of the numbers. Suppose that, in Year 0B, they find that they have not written down a counterexample. This indicates that the conjecture is true. However, due to their finite memory, they will only remember checking finitely many of the numbers. Can they assure themselves that they did in fact complete all of the calculations and didn’t give up partway through and sink into a decadent life of leisure? Again, there are possible remedies to this. They could set a computer on the task, putting precautions in place to make sure that the computer is not disturbed throughout the first  -sequence of years. This would be better but would run into similar objections. How could the person be sure that the computer’s integrity was maintained throughout its calculations, that it didn’t lose power partway through, that a rival mathematician didn’t hack into it, that it didn’t obtain consciousness and sink into a decadent life of leisure? Verifying that an infinite sequence of calculations was carried out correctly could take another infinity of years, in which case we are back to where we started. Such a proof of Goldbach’s Conjecture would be fundamentally different from any proofs done today, and it seems likely that its veracity would always be subject to some amount of doubt.
-sequence of years. This would be better but would run into similar objections. How could the person be sure that the computer’s integrity was maintained throughout its calculations, that it didn’t lose power partway through, that a rival mathematician didn’t hack into it, that it didn’t obtain consciousness and sink into a decadent life of leisure? Verifying that an infinite sequence of calculations was carried out correctly could take another infinity of years, in which case we are back to where we started. Such a proof of Goldbach’s Conjecture would be fundamentally different from any proofs done today, and it seems likely that its veracity would always be subject to some amount of doubt.

We will turn to some other esoteric thought experiments in our next post. Until then, here are some questions, essentially taken from Cody Gilmore’s “The Metaphysics of Mortals: Death, Immortality, and Personal Time,” to ponder in order to test your intuition. We’ll consider possible answers next time; feel free to post thoughts in the comment section.
- Alfred’s life has an external length of 100 years. However, his personal time passes very differently. The first 50 external years of his life correspond to his first personal year, the next 25 external years correspond to his second personal year, the next 12.5 external years to his third personal year, the next 6.25 to his fourth personal year, and so on. Is Alfred immortal?
- Betty’s life lasts for an entire
 -sequence of years of external time (in a world in which there is only one
-sequence of years of external time (in a world in which there is only one  -sequence). The first external year corresponds to one year of personal time, the second external year to half a year of personal time, the third external year to a quarter year of personal time, the fourth external year to an eighth of a year of personal time, and so on. Is Betty immortal?
-sequence). The first external year corresponds to one year of personal time, the second external year to half a year of personal time, the third external year to a quarter year of personal time, the fourth external year to an eighth of a year of personal time, and so on. Is Betty immortal?
- Carmen lives in a world with two
 -sequences of years. She is born during the first
-sequences of years. She is born during the first  -sequence of years, and her life lasts precisely until the end of the first
-sequence of years, and her life lasts precisely until the end of the first  -sequence of years. Her personal time matches external time. Is Carmen immortal?
-sequence of years. Her personal time matches external time. Is Carmen immortal?
- David lives in the same world as Carmen and is also born during the first
 -sequence of years, at the same time as Carmen. David lives through the end of the first
-sequence of years, at the same time as Carmen. David lives through the end of the first  -sequence of years and then five years into the second
-sequence of years and then five years into the second  -sequence of years before dying. His personal time matches external time. Is David immortal?
-sequence of years before dying. His personal time matches external time. Is David immortal?
Cover image: Salvador Dali, “The Persistence of Memory”
is a finite set of prime numbers. We will show that there is a prime number that is not in
. To do this, let
, and let
. For all
,
divides
with no remainder (as
), so, as
and
,
does not divide
. Since
and every integer greater than 1 has prime divisors, there is at least one prime,
, that divides
. But we just saw that no element of
divides
, so
is a prime that is not in
.
, let
, so
, etc. (
is known as the
Fermat number.)
,
.
be the smallest natural number such that
. Since the Claim can easily be verified by inspection for
, we may assume
. But now we have the following sequence of calculations where, because we are assuming that
is the smallest counterexample to the Claim, we can use the fact that
.
is not a counterexample to our Claim, contradicting our assumption and finishing the proof of the Claim.
and
are natural numbers,
is a prime, and
divides both
and
, then
divides
.
and
, where
and
are natural numbers. Then
, so
divides
.
are natural numbers, then there is no prime number
such that
divides both
and
.
and a prime number
such that
divides both
and
. Note that
is one of the factors in the product
, so
divides
. Since
, we also conclude that
divides
, so, by Claim 2, we know that
divides
. As
is prime, this means that
. But
and
are both odd, so this is impossible.
, choose a prime number
that divides
. By Claim 3, for all natural numbers
, we have
, so
is an infinite set of prime numbers.
is not prime. Indeed,
. Many mysteries remain regarding the Fermat numbers. For example, even the following two very basic questions remain unsolved to this day:
or
are prime. On the other hand, the truly gigantic number
is known to be non-prime: one of its prime factors is
.
, we have that
and
do not have any shared prime divisors. Now define an infinite sequence of natural numbers,
as follows. Let
be any natural number that is at least 2. Let
. Since
and
do not share any prime divisors, and since both
and
have at least one prime divisor, it follows that
must have at least 2 distinct prime divisors.
. Again,
and
do not have any shared prime divisors. We have shown that
has at least 2 distinct prime divisors, and we know that
has at least one prime divisor, so
must have at least 3 distinct prime divisors. Continuing in this way, defining
for every natural number
, one proves that, for each natural number
, the number
has at least
distinct prime divisors. In particular, there are infinitely many prime numbers.





