Month: July 2017

Tree decomposition in Budapest

I am spending this week in Budapest in order to participate in the 6th European Set Theory Conference, and I want to take the occasion to present a nice little result of Paul Erdős, one of the great mathematicians of the twentieth century, who was born and spent the first decades of his life in Budapest before spending most of his adult life traveling the world, living and working with a vast network of mathematical collaborators.

Erdős contributed to a huge array of mathematical disciplines, including set theory, my own primary field of specialization and the field from which today’s result is drawn. Like most other Hungarians working in set theory, Erdős’s results in the field have a distinctly combinatorial flavor.

In order to state and prove the result, we need to review a bit of terminology. Recall first that the Continuum Hypothesis is the assertion that the size of the set of all real numbers is \aleph_1, i.e., that there are no sizes of infinity strictly between the sizes of the set of natural numbers and the set of real numbers. As we have discussed, the Continuum Hypothesis is independent of the axioms of set theory.

The Continuum Hypothesis can be shown to be equivalent to a surprisingly diverse collection of other mathematical statements. We will be concerned with one of these statements today, coming from the field of graph theory. If you need a brief review of terminology regarding graphs, visit this previous post.

If Z is a set, then we say that the complete graph on Z is the graph whose vertex set is Z and which contains all possible edges between distinct elements of Z.

800px-Complete_graph_K7.svg
The complete graph on 7 vertices.

If G = (V, E) is a graph and k \geq 3 is a natural number, then a k-cycle in G is a sequence of k distinct elements of V, (v_1, v_2, \ldots, v_k), such that \{v_1, v_2\}, \{v_2, v_3\}, \ldots, \{v_{k-1}, v_k\}, \{v_k, v_1\} are all in E.

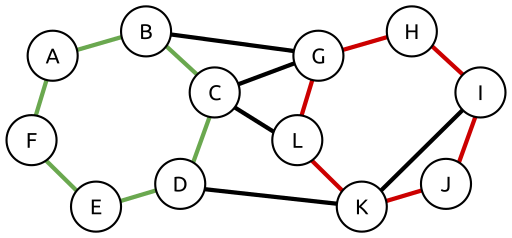
Graph_with_Chordless_and_Chorded_Cycles.svg
In this graph, both (A,B,C,D,E,F) and (G,H,I,J,K,L) form 6-cycles. (Image by Blacklemon67)

A graph without any cycles is called a tree. (Note that many sources require a tree to be connected as well as cycle-free and call a cycle-free graph a forest. This leads to the pleasing definition, “A tree is a connected forest.” We will ignore this distinction here, though.)

A complete graph is very far from being a tree: every possible cycle is there. We will be interested in the question: `How many trees does it take to make a complete graph?’

Let us be more precise. An edge-decomposition of a graph G = (V,E) is a disjoint partition of E, i.e., a collection of sets \{E_i \mid i \in I\}, indexed by a set I, such that E_i \cap E_j = \emptyset for distinct elements i,j \in I and \bigcup_{i \in I} E_i = E. An edge-decomposition thus decomposes the graph G = (V,E) into graphs G_i = (V, E_i) for i \in I.

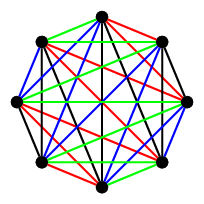
Walecki
An edge-decomposition of the complete graph on 8 vertices into 4 pieces, indicated by black, blue, green, and red edges, respectively.

We will be interested in the number of pieces required for an edge-decomposition of a complete graph into trees. In the above image, we provide an edge-decomposition of the complete graph on 8 vertices into 4 trees (in fact, into 4 Hamiltonian paths). For an infinite complete graph, though, no finite number of pieces will ever suffice. The question we will be interested in today is the number of pieces necessary to provide an edge-decomposition of the complete graph on the real numbers, \mathbb{R}, into trees.

Theorem. (Erdős-Kakutani and Erdős-Hajnal) The following statements are equivalent:

  1. The Continuum Hypothesis
  2. There is an edge-decomposition of the complete graph on \mathbb{R} into countably many trees.

Proof. Suppose first that the Continuum Hypothesis holds. Then \mathbb{R} can be enumerated as \langle r_\alpha \mid \alpha < \omega_1 \rangle. For all \beta < \omega_1, we know that \beta is countable, so we can fix a function e_\beta:\beta \rightarrow \mathbb{N} that is one-to-one, i.e., if \alpha_0 and \alpha_1 are distinct ordinals less than \beta, then e_\beta(\alpha_0) \neq e_\beta(\alpha_1).

We now specify an edge-decomposition of the complete graph on \mathbb{R} into countably many graphs. The edge-sets of these graphs will be denoted by E_n for n \in \mathbb{N}. To specify this decomposition, it suffices to specify, for each pair \alpha < \beta of countable ordinals, a natural number n_{\alpha, \beta} such that \{r_\alpha, r_\beta\} \in E_{n_{\alpha, \beta}}. And we have a natural way of doing this: simply let n_{\alpha, \beta} = e_\beta(\alpha).

We claim that each E_n is cycle-free. To prove this, suppose for sake of contradiction that k,n \in \mathbb{N} and E_n has a k-cycle. This means there are distinct ordinals \alpha_1, \alpha_2, \ldots, \alpha_k such that \{r_{\alpha_1}, r_{\alpha_2}\}, \{r_{\alpha_2}, r_{\alpha_3}\}, \ldots, \{r_{\alpha_{k-1}}, r_{\alpha_k}\}, \{r_{\alpha_k}, r_{\alpha_1}\} are all in E_n.

Now fix \ell \leq k such that \alpha_\ell is the maximum of the set \{\alpha_1, \ldots, \alpha_k\}. Without loss of generality, let us suppose that 1 < \ell < k (if this is not the case, simply shift the numbering of the cycle). Then we have \{r_{\alpha_{\ell - 1}}, r_{\alpha_\ell}\}, \{r_{\alpha_\ell}, r_{\alpha_{\ell + 1}}\} \in E_n. Since \alpha_\ell > \alpha_{\ell - 1}, \alpha_{\ell + 1}, our definition of E_n implies that e_{\alpha_\ell}(\alpha_{\ell - 1}) = n = e_{\alpha_\ell}(\alpha_{\ell + 1}), contradicting the assumption that e_{\alpha_\ell} is one-to-one and finishing the proof of the implication 1. \Rightarrow 2.

To prove that 2. implies 1., we will actually prove that the negation of 1. implies the negation of 2.. So, suppose that the Continuum Hypothesis fails, i.e., |\mathbb{R}| \geq \aleph_2. Let \langle r_\alpha \mid \alpha < |\mathbb{R}|\rangle be an enumeration of \mathbb{R}, and suppose \langle E_n \mid n \in \mathbb{N} \rangle is an edge-decomposition of the complete graph on \mathbb{R}. This means that, for all pairs of ordinals \alpha < \beta smaller than |\mathbb{R}|, there is a unique natural number n_{\alpha, \beta} such that \{r_\alpha, r_\beta\} \in E_{n_{\alpha, \beta}}. We will prove that there is a natural number n such that E_n contains a 4-cycle.

Let X be the set of ordinals that are bigger than \omega_1 but less than |\mathbb{R}|. Clearly, |X| = |\mathbb{R}| \geq \aleph_2. For each \beta \in X and each n < \omega, let A_{\beta, n} be the set of ordinals \alpha less than \omega_1 such that n_{\alpha, \beta} = n. Then \bigcup_{n \in \mathbb{N}} A_{\beta, n} = \omega_1, so, since \mathbb{N} is countable and \omega_1 is uncountable, there must be some natural number n such that A_{\beta, n} is uncountable. Let n_\beta be such an n.

For n \in \mathbb{N}, let X_n = \{\beta \in X \mid n_\beta = n\}. Then \bigcup_{n \in \mathbb{N}}X_n = X. Since |X| \geq \aleph_2, this means that there must be some natural number n^* such that |X_{n^*}| \geq \aleph_2.

Now, for each \beta \in X_{n^*}, let \alpha_{\beta, 0} and \alpha_{\beta, 1} be the least two elements of A_{\beta, n^*}. Since there are only \aleph_1 different choices for \alpha_{\beta, 0} and \alpha_{\beta, 1}, and since |X_{n^*}| \geq \aleph_2, it follows that we can find \beta_0 < \beta_1 in X_{n^*} and \alpha_0 < \alpha_1 < \omega_1 such that \alpha_{\beta_0, 0} = \alpha_0 = \alpha_{\beta_1, 0} and \alpha_{\beta_0, 1} = \alpha_1 = \alpha_{\beta_1, 1}. It follows that \{r_{\alpha_0}, r_{\beta_0}\}, \{r_{\beta_0}, r_{\alpha_1}\}, \{r_{\alpha_1}, r_{\beta_1}\}, \{r_{\beta_1}, r_{\alpha_0}\} \in E_{n^*}. In other words, (r_{\alpha_0}, r_{\beta_1}, r_{\alpha_1}, r_{\beta_1}) forms a 4-cycle in E_{n^*}. This completes the proof of the Theorem.

Notes: The proofs given here do not exactly match those given by Erdős and collaborators; rather, they are simplifications made possible by the increased sophistication in dealing with ordinals and cardinals that has been developed by set theorists over the previous decades. The implication from 1. to 2. is due to Erdős and Kakutani and can be found in this paper from 1943. The implication from 2. to 1. was stated as an unsolved problem in the Erdős-Kakutani paper. It was proven (in a much more general context) in a landmark paper by Erdős and Hajnal from 1966.

Posted on by Chris Lambie-Hanson 2