Why should anyone be frightened by a hat?
-Antoine de Saint-Exupéry
As a traveling mathematician, one steadily amasses, mostly over drinks with other mathematicians, a compendium of puzzles, conundrums that come to us from some strange world of transfinite subways and unnecessarily complicated lighting solutions.
One of the most common types of puzzle one encounters in this way is the “hat puzzle,” which typically involves a situation of the following form: some number of people are wearing hats. According to the prevailing fashions in this world, each hat is either red or blue. Some of these people can see the hats of some of the other people, but nobody can see their own hat. The most common way to make this plausible is to suppose that these people are prisoners at the whims of some sadistic prison warden who has buried them up to their necks so that they do not have use of their arms to reach up, remove their hats, and examine their color. The people want to guess the colors of their own hats in order to gain their freedom (the rules and winning conditions of the contest vary according to the puzzle under consideration). Your challenge is typically to come up with the optimal strategy for the prisoners to employ so that they have the highest chance of escaping or so that as many of them as possible are guaranteed to escape.
Hat puzzles come in two basic flavors that look similar in setup but feel very different in execution: puzzles with finitely many hat-wearers and puzzles with infinitely many hat-wearers. Solutions to finite hat puzzles typically involve finding clever ways to encode or transmit information. Solutions to infinite hat puzzles typically involve finding clever applications of the axiom of choice. And though Point at Infinity is dedicated to all things infinite, I don’t want to deprive my readers of the joys of finite hat puzzles, so, over the next two weeks, we will look at both. This week will cover the finite case, with two basic puzzles today and a more involved one, with connections to information theory, on Thursday.
Puzzle One: The Four Hats
There are four prisoners, named A,B,C, and D. Each is wearing either a blue or a red hat, and each knows that there are two hats of each color between them. The prisoners are all buried up to their necks. A,B, and C are in a line on one side of a brick wall, so that A can see B and C, B can only see C, and C can see neither of the others. D is on the other side of the brick wall; they can see nobody else, and nobody can see them. The prisoners are not allowed to speak except to guess the color of their own hat. If the first prisoner to speak guesses their own hat color correctly, then all four go free. If the first prisoner to speak guesses their own hat color incorrectly, then all four are executed. Can the prisoners guarantee their release?
(ANSWER AFTER THE PICTURE. TAKE A MOMENT TO THINK BEFORE READING FURTHER.)

Yes, the prisoners can guarantee success. Here’s how.
- First note that, if B and C have the same color hat, then A will know this. A will then know that there are no more hats of that color, since everyone knows there are only two hats of each color. A can then confidently declare the other color.
- If B and C have different hat colors, then A can no longer be sure of the color of their hat. A will therefore be silent. After a short period of silence, B will be able to conclude that their hat color is different from C’s, as otherwise A would have immediately spoken. B can therefore confidently state the color that C is not wearing.
This covers all of the possible configurations of hats, so we are done!
Puzzle Two: The Ten Hats
That was just a warm-up. Let’s get to something more interesting. In this puzzle, there are ten prisoners (as we will see, the exact number is not important; the solution will generalize to any number of prisoners), numbered 1 through 10. They are each wearing a hat, either red or blue, randomly assigned. Each prisoner knows that all of the hats are either red or blue, but none of them knows how many hats of each color there are. The prisoners are again buried up to their necks in a straight line, this time in a way so that each prisoner can see exactly those prisoners with higher numbers.
The warden proceeds along the line, from back to front (1 to 10), asking each prisoner to guess the color of their own hat. The guesses are audible to all of the prisoners, but no other communication is permitted. (The prisoners were permitted to confer and devise a strategy before they were buried and given hats, though). For each prisoner, if they guess their hat color correctly, then they are released. If they guess incorrectly, then they are executed. How should the prisoners act to maximize the number of prisoners who are guaranteed to be released?
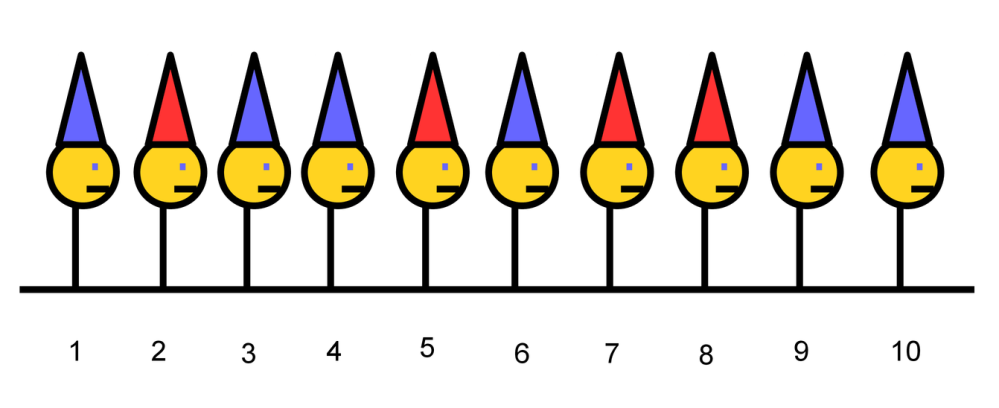
Here’s a first natural attempt at a solution. Suppose that each odd-numbered prisoner guesses the color of the prisoner in front of them. Then each even-numbered prisoner will hear this guess and know the color of their own hat, so they can simply repeat the guess of the prisoner behind them. This will guarantee that each even-numbered prisoner is released. In addition, some of the odd-numbered prisoners will get lucky and ‘accidentally’ guess their own color. Half of the prisoners are guaranteed to be released, and, on average, three-quarters of the prisoners will be released. Can we do better?
Yes! First, note that Prisoner 1 is always guessing with no information and thus cannot have better than a 50 percent chance of being released. The best we can possibly do, then, is to guarantee that the other nine prisoners can be released. This might seem, at first, hopelessly optimistic, but it can be achieved!
The key idea is that, through their guesses, the prisoners can pass up information about how many red or blue hats they can see, while simultaneously (except for Prisoner 1) guessing their own hat colors correctly. To get things started, it is agreed among the prisoners that Prisoner 1 will guess ‘Red’ if they see an even number of red hats and ‘Blue’ if they see an odd number of red hats. Let’s first see how this helps Prisoner 2.
After Prisoner 1’s guess, Prisoner 2 knows whether Prisoner 1 saw an even or odd number of red hats. Prisoner 2 also knows whether they themselves see an even or odd number of red hats. If the prisoners agree about this information, then Prisoner 2 knows that they must be wearing a blue hat and will guess ‘Blue.’ If they disagree about this information, then Prisoner 2 knows that they must be wearing a red hat and will guess ‘Red.’
Here’s how this will play out in the particular instance of the puzzle in the picture above. Prisoner 1 sees 4 red hats (and 5 blue hats) and will therefore say ‘Red,’ signifying an even number of red hats. Prisoner 2 sees 3 red hats, an odd number. Prisoner 2 therefore knows that, to account for the discrepancy between what they see and what Prisoner 1 sees, they must be wearing a red hat and will say ‘Red.’
Here’s the neat part: when Prisoner 2 guesses their hat color (correctly), they are simultaneously telling the other prisoners whether they see an even or an odd number of red hats, since their guess depends on whether what they see agrees or disagrees with what Prisoner 1 sees. Prisoner 3 is now in the same position as Prisoner 2 was after Prisoner 1 had guessed, so Prisoner 3 can guess correctly. But now Prisoner 3 is telling the other prisoners whether they see an even or odd number of red hats, and Prisoner 4 can guess correctly. This continues all the way up the line, and Prisoners 2 through 10 all escape.
Let’s go back to the picture to see how this would work in this particular instance. We know that Prisoner 1 says ‘Red,’ and then Prisoner 2 correctly guesses ‘Red.’ What does Prisoner 3 know now? They know that Prisoner 1 saw an even number of Red hats, because Prisoner 1 said ‘Red.’ They then know that Prisoner 2 saw an odd number of Red hats, because they also said ‘Red.’ Prisoner 3 sees an odd number (3) of red hats, which agrees with what Prisoner 2 sees. Therefore, Prisoner 3 knows their hat is blue and says ‘Blue.’ Prisoner 4 then knows that Prisoner 3 sees an odd number of red hats. Prisoner 4 also sees an odd number of red hats, so Prisoner 4 guesses ‘Blue.’ Prisoner 5 sees an even number of red hats. Since this disagrees with what they know Prisoner 4 sees, they guess ‘Red,’ and so on.
As I mentioned, it is clear that this solution does not depend on there being exactly ten prisoners; it will work for any number of prisoners who happen to find themselves in the same position. The first prisoner will be in the unfortunate situation of having only a 50 percent chance of escaping, but the remaining prisoners can all be guaranteed escape!


2 thoughts on “Finite Hats”