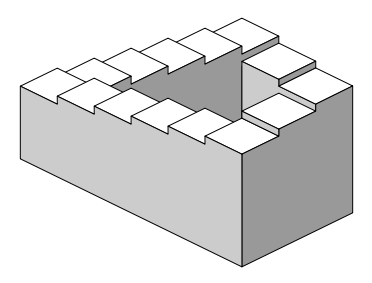
Welcome one, welcome all to the Point at Infinity sideshow, where today we present a tantalizing and diabolical selection of musical and mathematical curiosities. Just watch your step; these stairs can be a bit tricky.

A few months ago, you may recall, we published two posts about the Shepard tone and the Risset rhythm, aural illusions in which a tone or rhythm seems to perpetually rise or fall in pitch or in tempo but is actually repeating the same pattern over and over again, the musical equivalents of Penrose stairs.

372px-Impossible_staircase.svg
Penrose stairs. (Image in the public domain.)

To accompany the posts we created some sound samples so the readers could hear the illusions themselves. A couple of weeks ago, one of these samples was used in an internet radio program on audio paradoxes released by Eat This Radio, paired with some work of Jean-Claude Risset. The entire program is really excellent, ranging from a piece by J.S. Bach to mid-twentieth century audio experiments to modern electronic music, and I encourage all of you to listen to it.

One of the pieces in the radio program is a piano étude written by György Ligeti in the late twentieth century. The étude is named L’escalier du diable, or The Devil’s Staircase, and its repeated ascents of the keyboard have a striking resonance with the never-ending ascent of the Shepard tone.

The Devil’s Staircase is also the colloquial name given to a particular mathematical function introduced by Georg Cantor in the 1880s. It is a function defined on the set of real numbers between 0 and 1 and taking values in the same interval, and it has some quite curious properties. Before we discuss it, let’s take a look at (an approximation to) the graph of the function.

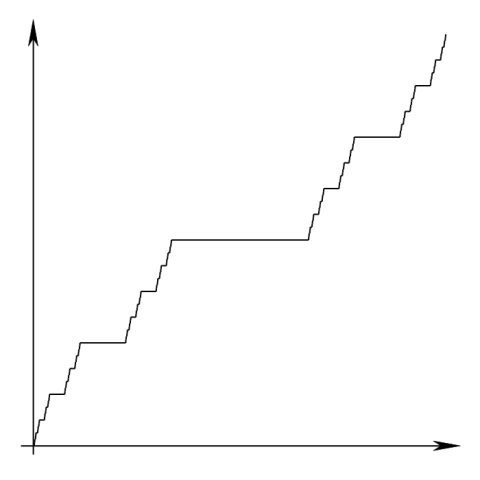
CantorEscalier.svg
Graph of the Devil’s Staircase. By Theon, CC BY-SA 3.0.

To appreciate the strangeness of this function, let us recall some definitions regarding functions of real numbers. Very roughly speaking, a function is called continuous if it has no sudden jumps, or if its graph can be drawn without lifting the pencil from the page. Continuous functions satisfy a number of nice properties, such as the intermediate value theorem.

The derivative of a function at a given point of its domain, if it exists, measures the rate of change of the function at that point. If the x-axis measures time and the y-axis measures the position of an object along some one-dimensional track, then the derivative can be thought of as the velocity of that object. If a function is differentiable at a point (i.e., if its derivative exists there) then it must be continuous at that point, but the converse is not necessarily true. (For example, if the graph of a function has a sharp corner at a point, then the function cannot be differentiable there.)

Let’s think about what it means for a function to have a derivative of 0 at a point. It means that, at that point, the rate of change of the function has vanished. It means that, if we zoom in sufficiently close to that point, the function should look like a constant function. Its graph should look like a horizontal line. What would it mean for a function to have a derivative of 0 almost everywhere? (Here “almost everywhere” is a technical term (which I’m not going to define) and not just me being vague.) One might think that this must imply that the function is a constant function. At almost every point in its domain, the rate of change of the function is 0, so how can the value of the function change?

One will quickly discover that this is not quite right. Consider the function defined on the real numbers whose value is 0 at all negative numbers and 1 at all non-negative numbers.

step

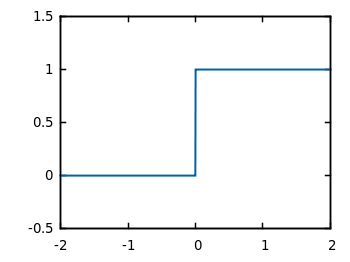
This function has derivative 0 everywhere except at 0 itself, and yet it increases from 0 to 1. It does this quite easily by being discontinuous at 0, which, in hindsight, seems sort of like cheating. So what if we also require our function to be continuous? Now we need more exotic examples, and this is where the Devil’s Staircase comes in, for the Devil’s Staircase is a continuous function, it is differentiable almost everywhere, it has a  derivative of 0 wherever its derivative is defined, and yet it still manages to increase from 0 to 1. Wild!

What is the Devil’s Staircase exactly? I’ll give two different definitions. The first proceeds via an iterative construction. Start with the function f_0(x) = x. Its graph, between 0 and 1, is simply a straight line segment increasing from (0,0) to (1,1). Now, look at the midpoint of this increasing line segment, and draw a horizontal line segment centered there whose length is 1/3 of the horizontal line of the original increasing segment. Now connect the ends of this line segment via straight lines to (0,0) and (1,1). This new curve is the graph of a function that we call f_1. It consists of two increasing line segments with one horizontal line segment between them. Now repeat the process that took us from f_0 to f_1 on each of these increasing line segments, and let f_2 be the function whose graph is the result. Continue in this manner, constructing f_n for every natural number n.

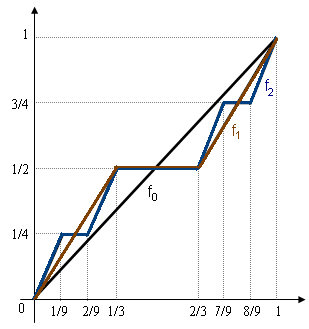
Cantor_function_sequence
First three steps of the iterative construction of the Devil’s Staircase. (Image in the public domain.)

It turns out that, as n goes to infinity, the sequence of functions \langle f_n \mid n \in \mathbb{N} \rangle converges (uniformly) to a single function. This function is the Devil’s Staircase.

A more direct but also more opaque definition is as follows: Given a real number x between 0 and 1, first express x in base 3 (i.e., using only 0s, 1s, and 2s). If this base 3 representation contains a 1, then replace every digit after the first 1 with a 0. Next, replace all 2s with 1s. The result has only 0s and 1s, so we can interpret it as a binary (i.e., base 2) number, and we let f(x) be this value. Then the function f defined in this manner is the Devil’s Staircase. Play around with this definition, and you might get a feel for what it’s doing.

And now, on our way out, some musical addenda. An encore, if you will. First, after making the Risset rhythms for the aforementioned post, I did some further coding and wrote a little program that can take any short audio snippet and make a Risset rhythm out of it. Here’s an example, first accelerating and then decelerating, using a bit from a Schubert piano trio.

You may recognize the sample from the soundtrack to Barry Lyndon.

Finally, I can’t help but include here one of my favorite pieces by Ligeti, Poema sinfónico para 100 Metrónomos.

Cover image: Devil’s Staircase Wilderness, Oregon, USA

3 thoughts on “L’escalier du Diable”

  1. Pingback: Introducing The Humming of the Strings – Point at Infinity
  2. Pingback: Welcome to The Humming of the Strings – The Humming of the Strings
  3. Pingback: Montées et descentes infernales : dans l’escalier de Ligeti – Les autocrates

Leave a comment